Morpho Manual

The meshgen module

The meshgen module conveniently produces high quality meshes for many kinds of domain. It follows the builder pattern with a MeshGen helper object that performs the construction. To use meshgen, the user must provide a scalar function that is positive everywhere that they want to be meshed.

Note One example is referred to in the literature as a signed distance function, which is the Euclidean distance of a given point \(x\) to the boundary of a set \(\Omega\) with the sign positive if \(x\) is in the interior of \(\Omega\). MeshGen does not require signed distance functions, but accepts any continuous and reasonably smooth function.

For example, the interior of the unit disk in two dimensions, is described by the function $$f(x,y)=1-(x^{2}+y^{2}).$$ To create the corresponding Mesh, we must first specify a suitable morpho function that describes the domain. This function will be called repeatedly by MeshGen, which will pass it a position vector x. Hence, the \((x,y)\) components must be accessed from the argument x by indexing:

fn disk(x) {
    return 1-(x[0]^2+x[1]^2)
}

Now that the function is specified, we can create a MeshGen object:

var mg = MeshGen(disk, [-1..1:0.2, -1..1:0.2])

The second parameter is a list of Ranges that provide overall bounds on the domain to be meshed. Here we will use \(x,y\in[-1,1]\). By setting the stepsize, the user can provide MeshGen with an overall suggestion of the resolution.

Finally, we create the Mesh by calling the build method:

var m = mg.build();

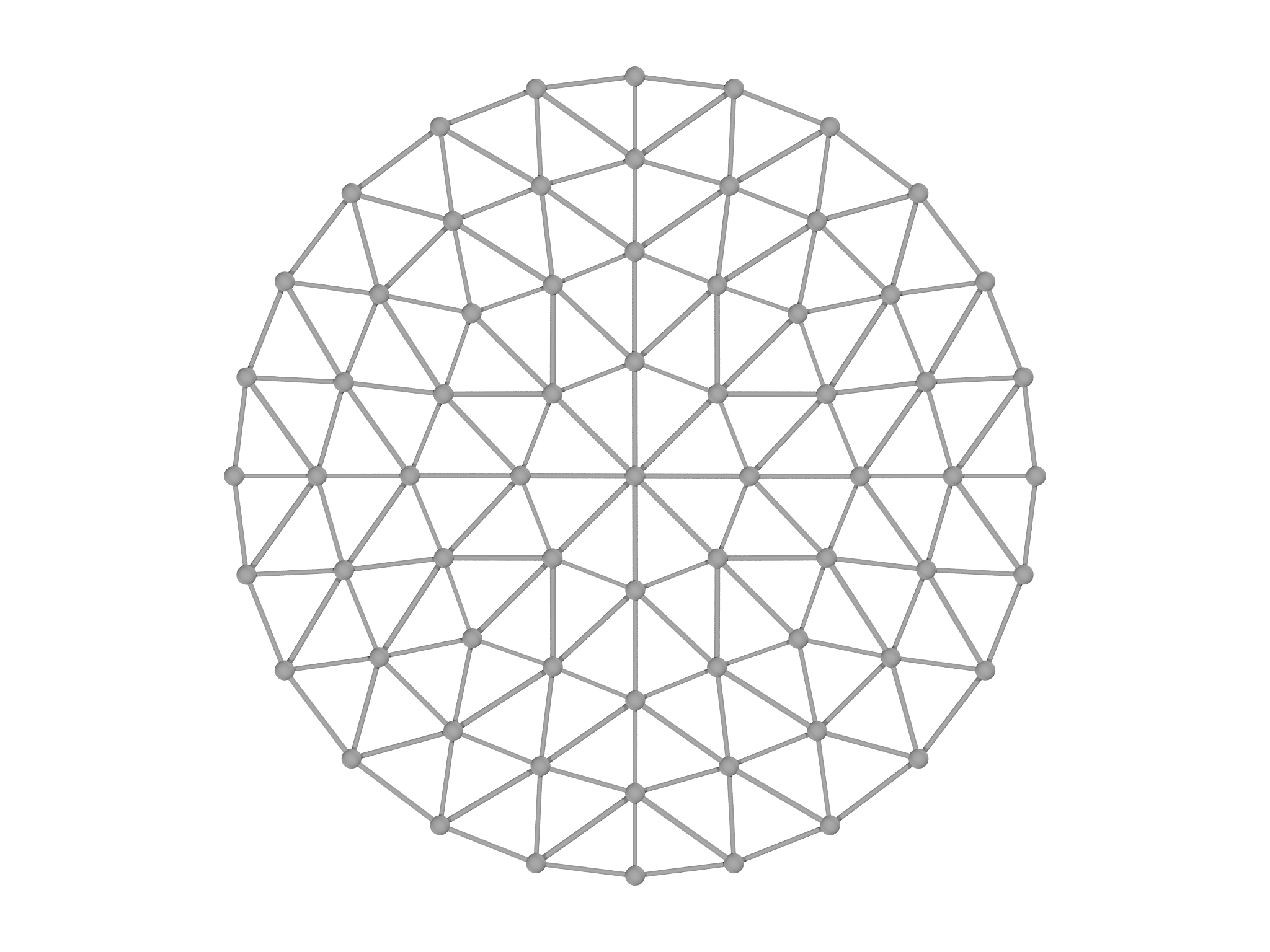
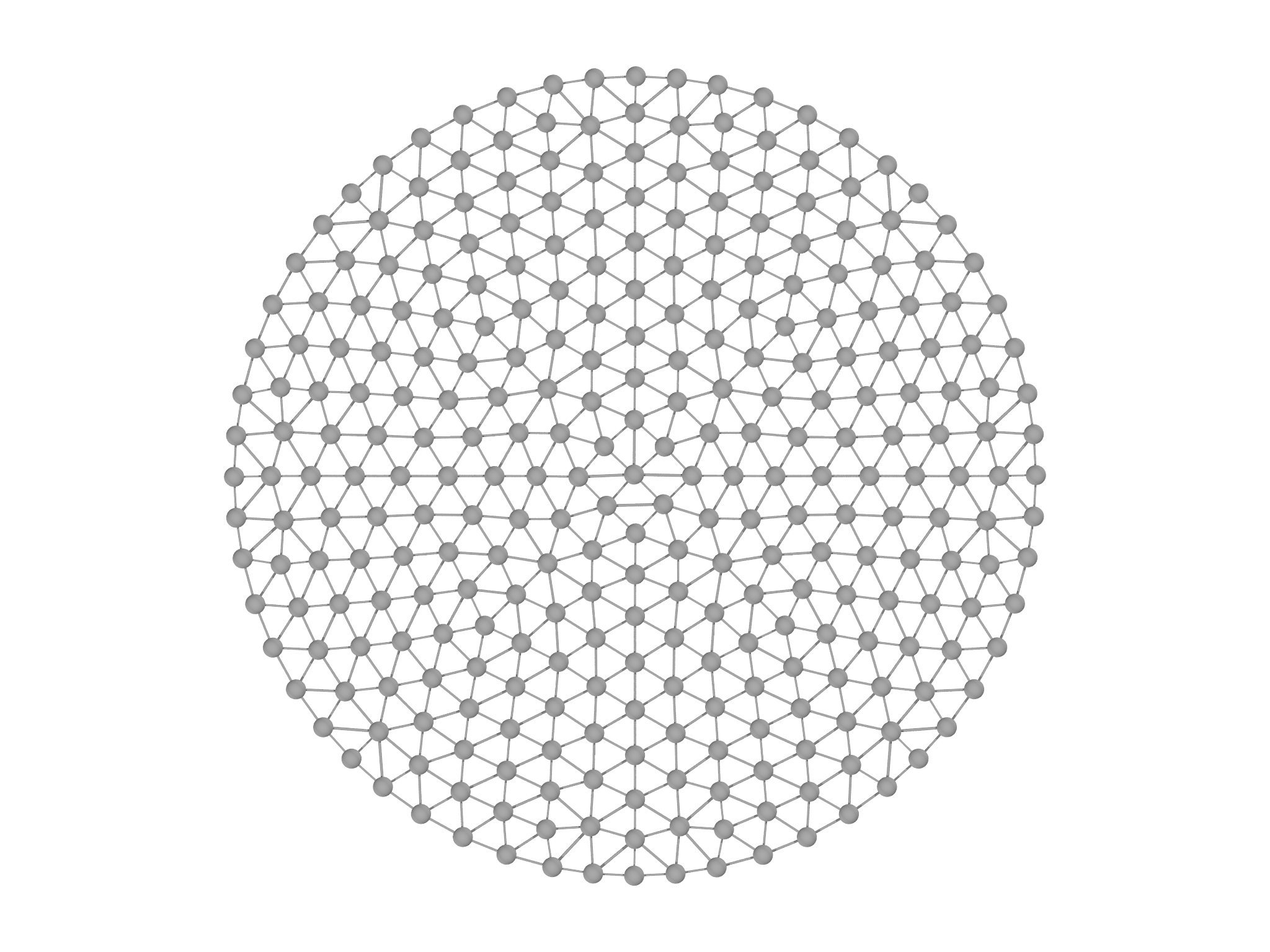
The resulting Mesh is shown in Fig. 5.1, left panel. A higher resolution Mesh can be generated by changing the Range objects passed to MeshGen:

var mg = MeshGen(disk, [-1..1:0.1, -1..1:0.1])

This generates a much higher resolution Mesh, with approximately four times the number of vertices as shown in Fig. 5.1, right panel.

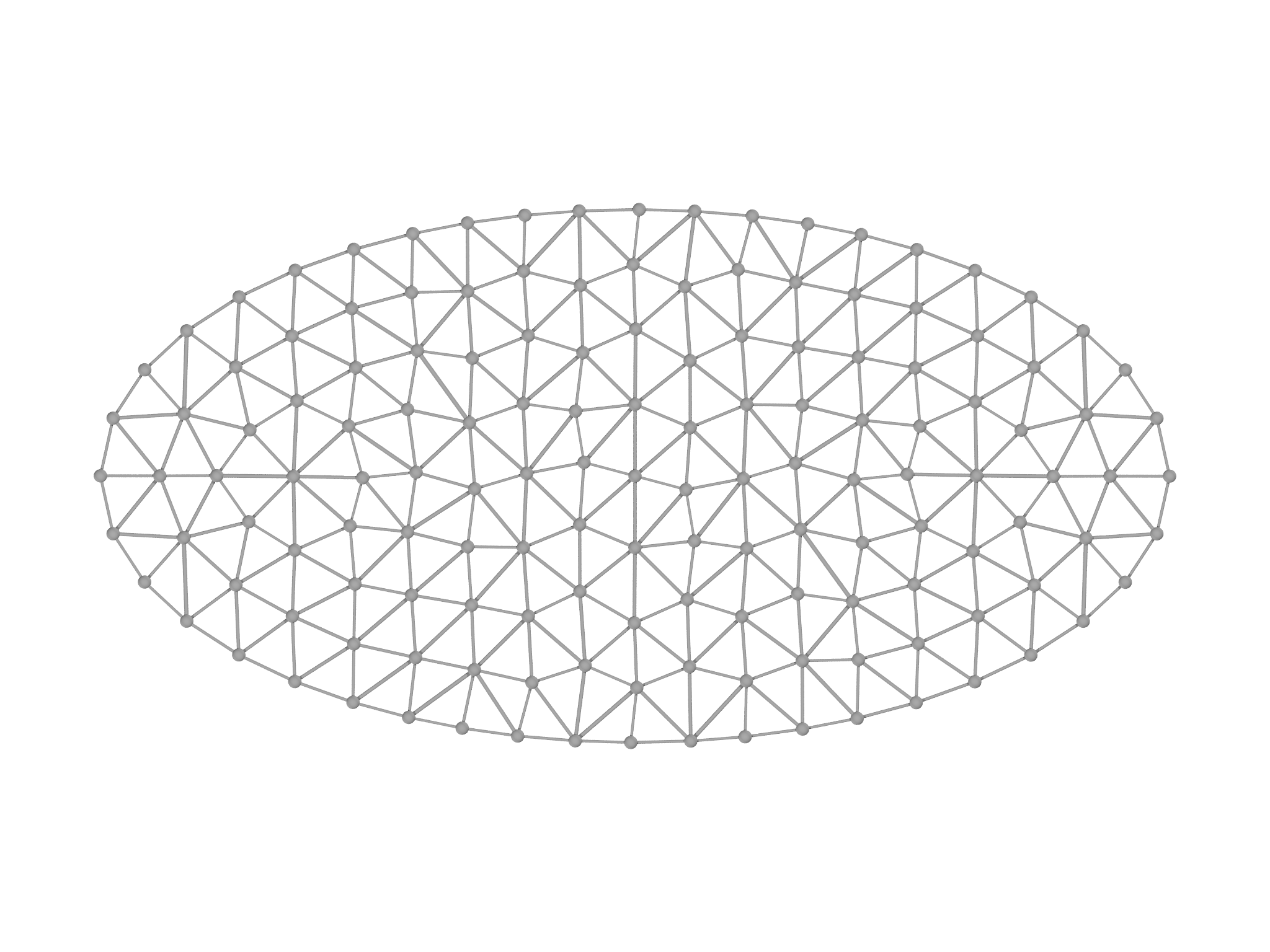
MeshGen can also mesh more complicated domains. To facilitate this, it provides a Domain class that accepts a scalar function in its constructor. For example, this code creates an ellipse as shown in Fig. 5.2, left panel:

var e0 = Domain(fn (x) -((x[0]/2)^2+x[1]^2-1))
var mg = MeshGen(e0, [-2..2:0.2, -1..1:0.2])
var m = mg.build()

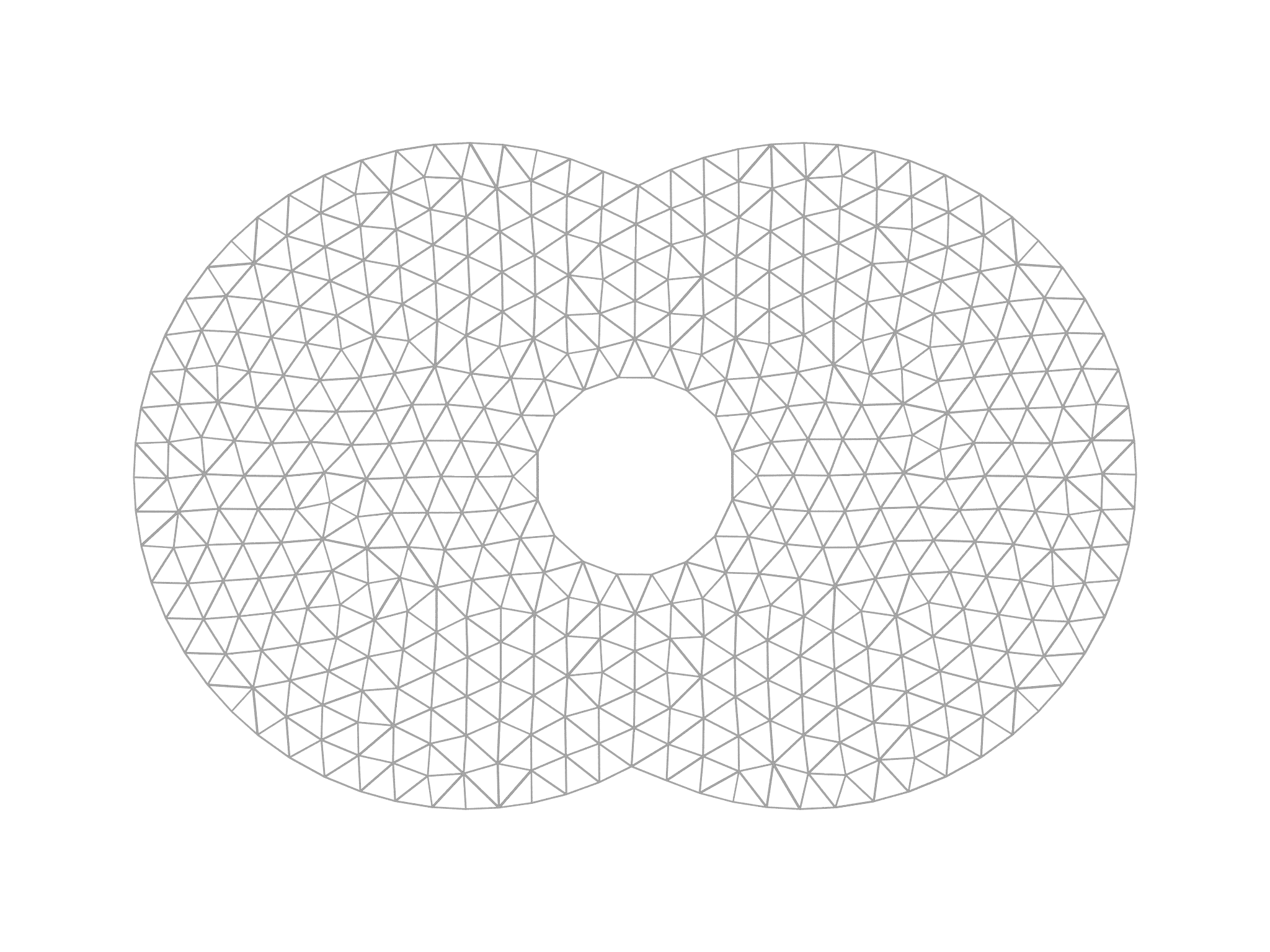
The benefit of this is that Domain objects can be combined using set operation methods union, intersection and difference. To illustrate the possibilities with this, we use a special constructor to create three domains corresponding to disks,

var a = CircularDomain(Matrix([-0.5,0]), 1)
var b = CircularDomain(Matrix([0.5,0]), 1)
var c = CircularDomain(Matrix([0,0]), 0.3)

then combine them,

var dom = a.union(b).difference(c)

and mesh the resulting domain,

var mg = MeshGen(dom, [-2..2:0.1, -1..1:0.1], quiet=false)
var m = mg.build()

with the result shown in Fig. 5.2, right panel.

Three dimensional meshes are created very similarly. Here we create a spherical mesh, displayed in Fig. 5.3

var dh = 0.2
var dom = Domain(fn (x) -(x[0]^2+x[1]^2+x[2]^2-1))
var mg = MeshGen(dom, [-1..1:dh, -1..1:dh, -1..1:dh])
var m = mg.build()