Catenoid

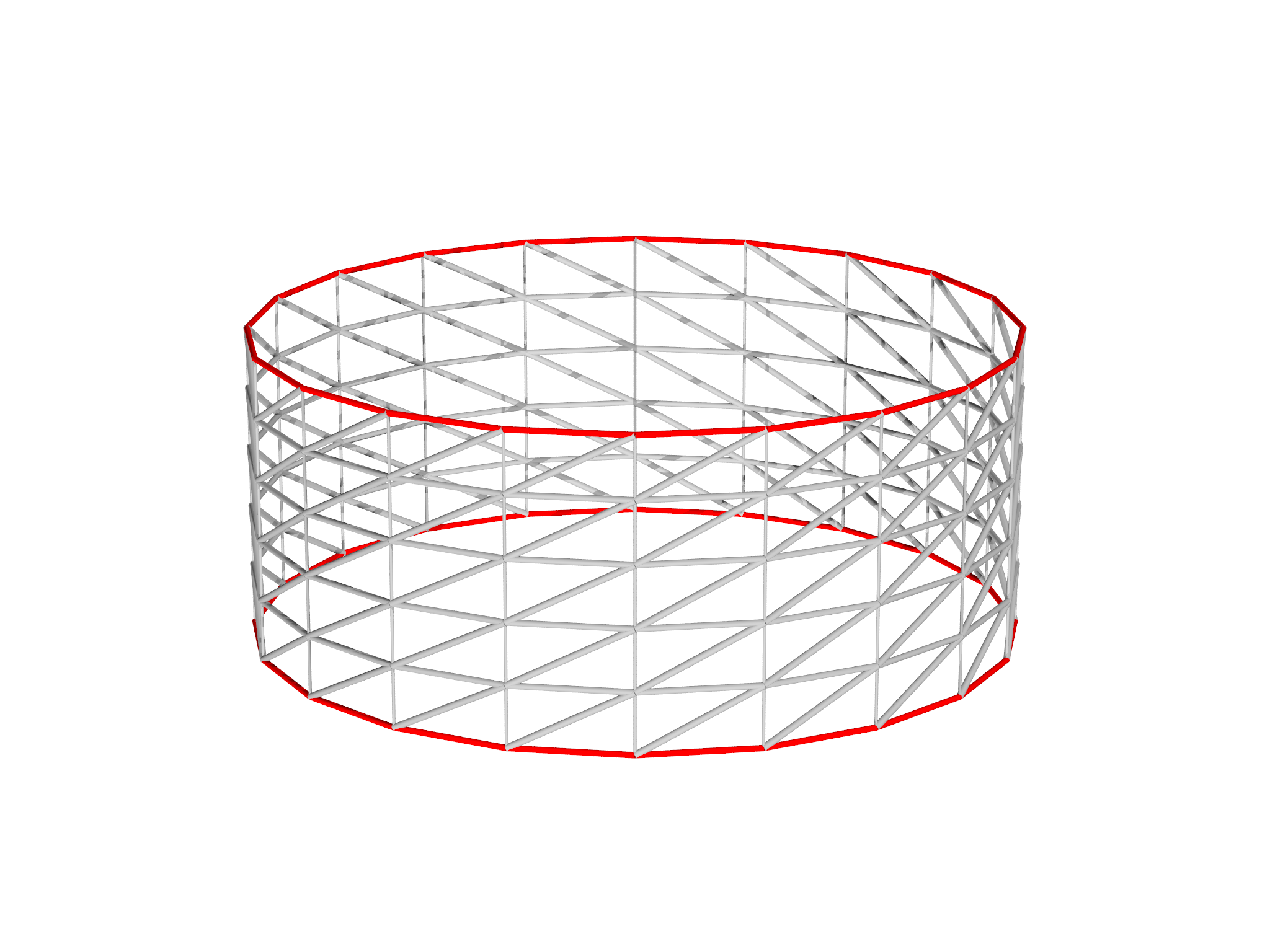
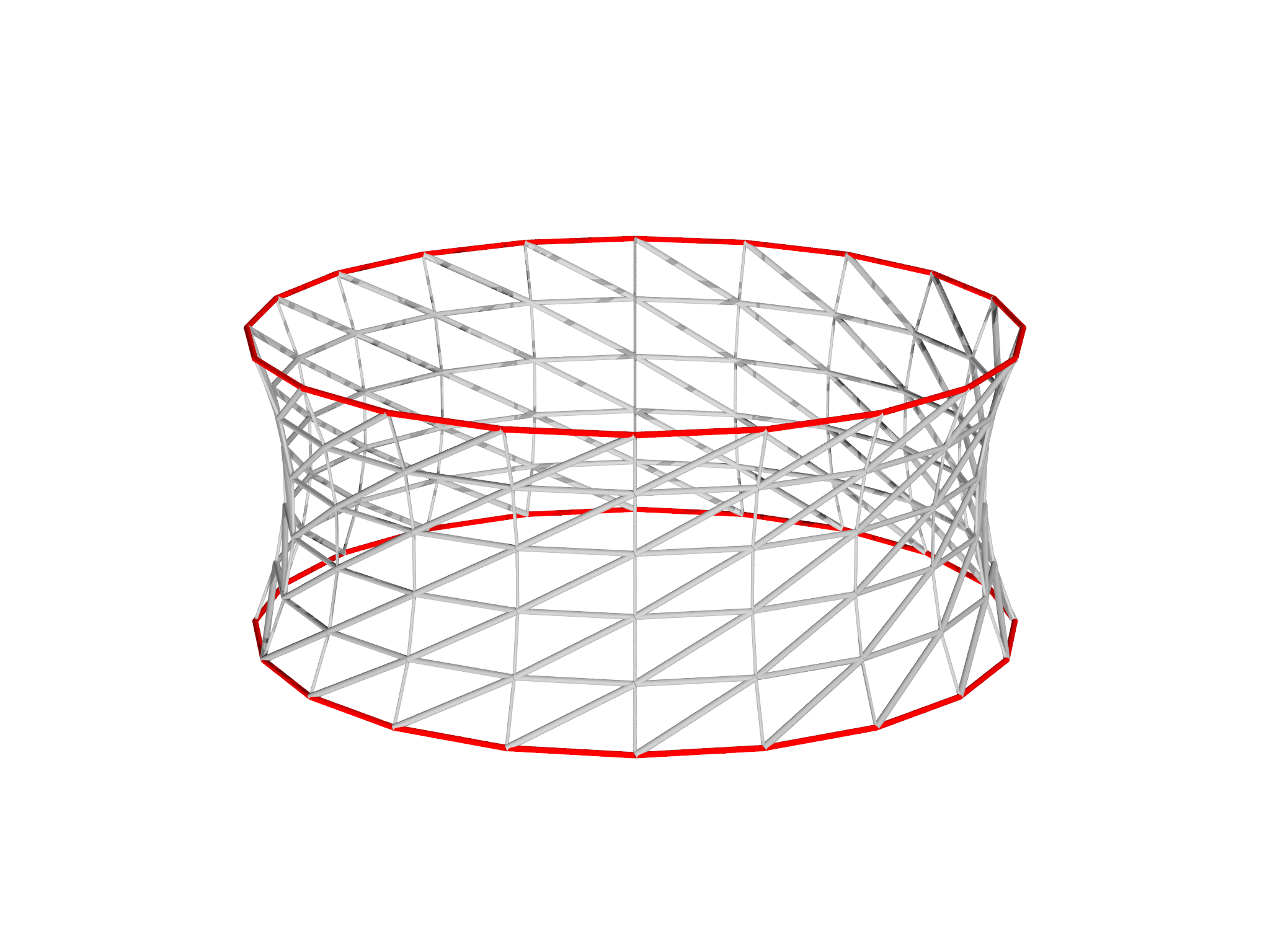
imageimage

Catenoid. (left) initial mesh before optimization and (right) after optimization. Only grade 1 elements are shown. Boundary elements are displayed in red.

A soap film held between two parallel concentric circular rings adopts the shape of a minimal surface called a catenoid. This is a relatively simple optimization problem, and hence is a good example for beginners to morpho.

The initial mesh is created using AreaMesh in the meshtools module:

var r = 1.0 // radius
var ratio = 0.4 // Separation to diameter ratio
var L = 2*r*ratio // Separation

// Generate a tube / cylindrical mesh
var mesh = AreaMesh(fn (u, v) [r*cos(u), v, r*sin(u)],
                    -Pi...Pi:Pi/10,
                    -L/2..L/2:L/5,
                    closed=[true,false] )
mesh.addgrade(1)

The boundary of the mesh must be fixed in place. We can do this by creating a Selection, and visualizing it as shown in Fig. 7.1, left panel:

// Select the boundary
var bnd = Selection(mesh, boundary=true)
var g = plotselection(mesh, bnd, grade=1)

The optimization problem simply requires us to specify the area as the quantity to minimize:

 // Define the optimizataion problem
var problem = OptimizationProblem(mesh) 
// Add the area energy using the built-in Area functional
var area = Area()
problem.addenergy(area)

We then create a ShapeOptimizer to perform the optimization,

var opt = ShapeOptimizer(problem, mesh)

fix the boundary elements using the selection object we created,

opt.fix(bnd)

and perform the optimization. Conjugate gradient works well for this problem and converges in a few iterations. The final optimized shape is shown in Fig. 7.1, right panel.

opt.conjugategradient(1000)